Can Mathematics Help Patients with Burn Injuries?
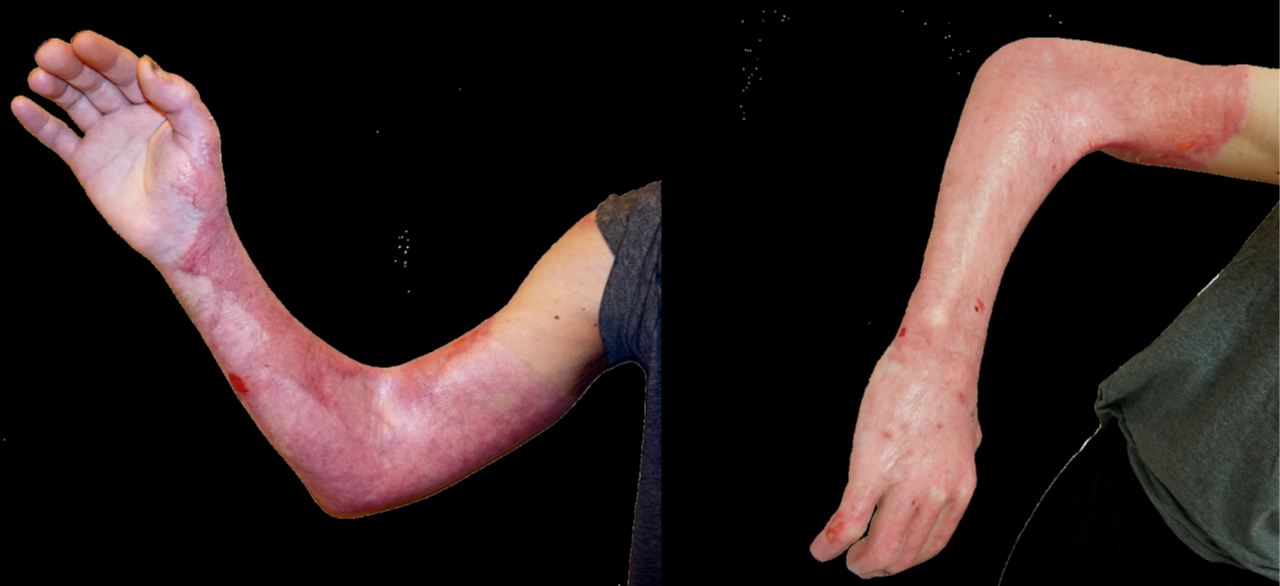
Every day, about 33,000 people throughout the world suffer heavy burn injuries that often dramatically change their lives. These individuals require sophisticated health care and are often subject to physiological (mobility) limitations even after they heal; in many cases, there is also a significant psychological impact. The formation of hypertrophic scars may alter a patient’s appearance, dermal contractions may limit joint mobility, and contractures—a tightening and hardening of muscles, tendons, and tissues—might impede overall mobility. Such mobility limitations can range from preventing active participation in sporting events to restricting daily tasks like walking, cooking, or other household activities. Figure 1 illustrates a contraction after a burn injury.
Because the survival rate of patients with severe burn injuries has improved tremendously in recent years, health care efforts are now focusing on bettering patients’ quality of life by preventing and/or mitigating the formation of contractures and hypertrophy. Possible treatments include dressings, ointments, and bandages, but severe burns frequently necessitate skin grafts wherein a surgeon removes a person’s damaged (dead) skin and replaces it with skin from undamaged body segments. Depending on the location and severity of the burn, skin grafting can take several forms [9].
In order to optimize burn treatment, we must understand the qualitative relationships between biological parameters and processes within the burned skin. Mathematical models can lend necessary predictive insight and forecast the expected scenarios for post-burn dermal evolution. A modeling framework that accounts for therapies could help practitioners identify treatments that successfully minimize—or even prevent—contraction and hypertrophy. Our long-term objective is to formulate a computational model that is applicable in a clinical environment.
Mathematical Framework
After a burn occurs, the immune system sends white blood cells (macrophages, leukocytes, T-cells, and so forth) to the damaged skin in order to clear up the debris. These cells secrete chemokines that attract the nearby fibroblasts, which are located in the undamaged skin and under the injured skin. The fibroblasts migrate into the damaged skin region and start to secrete and deposit collagen to restore the skin. Due to the balance of certain chemokines and localized mechanical stresses, fibroblasts often turn into myofibroblasts that still produce collagen but also exert relatively large forces on their immediate environments, causing the wound to contract. Furthermore, the large quantities of collagen that the myofibroblasts produce have a different composition and dissimilar mechanical properties than the embryonic collagen from fibroblasts.
Our mathematical framework is based on a continuum formalism that is applicable on the scale of tissues, which fall in the range of centimeters to decimeters. We thus model cells (fibroblasts and myofibroblasts), collagen, and chemicals in terms of their densities, which are solutions to conservation laws that are formulated by partial differential equations (PDEs). These PDEs involve random walks (diffusion), chemotaxis (migration in the direction of a chemokine’s gradient), cell differentiation, cell proliferation (division), and cell death. We also account for the regeneration and deposition of collagen, as well as the secretion of chemokines for intracellular communication. If \(c\) is an entity’s density, then the typical form of such a conservation law is \[\frac{D c}{D t} + c ~ (\nabla \cdot {\mathbf v}) + \nabla \cdot J(c) = f(c).\tag1\]
Here, \(J(c)\) and \(f(c)\) respectively denote the flux (due to random walks, passive convection, and chemotaxis) and accumulation (due to processes like proliferation, death, and differentiation or regeneration). Additionally, \(\mathbf{v}\) denotes the displacement velocity as a result of cell forces and \(\frac{D}{Dt}(.)\) denotes the material derivative. In addition to the conservation of these biochemical entities, we also note the effects of conservation of momentum. This balance reads as \[\rho \left(\frac{D {\mathbf v}}{D t} + {\mathbf v} ~ (\nabla \cdot {\mathbf v}) \right) - \nabla \cdot \sigma = \rho ~{\mathbf F},\tag2\]
where \(\rho\), \(\sigma\), and \(\mathbf F\) respectively denote the mass density of the tissue, stress tensor, and body force as a result of the pulling forces that the myofibroblasts exert. We couple this equation to the other PDEs and to another evolutionary equation for the effective Eulerian strain [1, 3]. This set of mechanical model equations is called a morphoelastic framework; it combines mechanical displacements, strains, and stresses with tissue shrinkage due to microstructural changes.
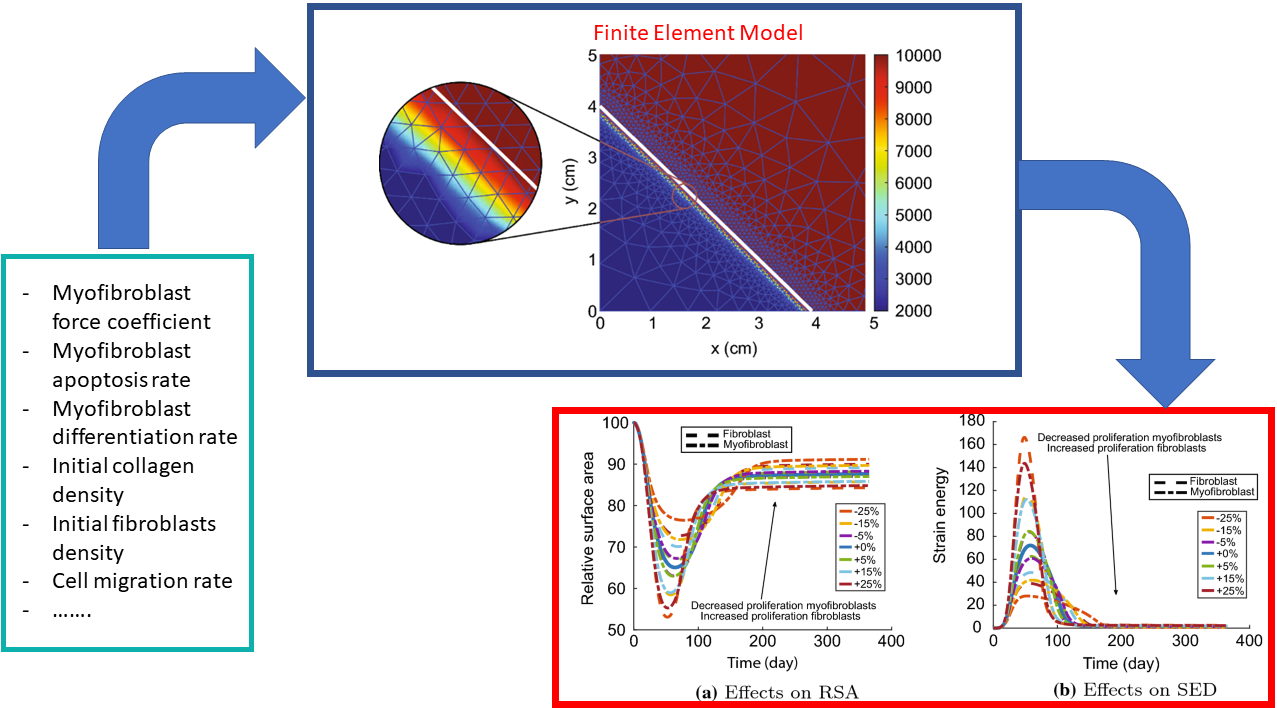
The PDEs contain many input parameters that are patient-specific and/or poorly documented. Moreover, the initial region of a burn injury is not well known because examination of the wound area only begins once the patient has received the first round of essential care. All of these factors cause uncertainty that impacts both post-burn dermal evolution and modeling outcomes. We therefore conduct uncertainty quantification by estimating the probability distributions of the most relevant output parameters, such as the extent of skin contraction and the total amount of strain energy (which we can use to quantify the overall degree of agony that the patient experiences). We compute each sample run from the model by sampling the input parameters from prior statistical distributions and solving the set of nonlinearly coupled PDEs via a combination of moving finite elements, time integration, the fixed-point method, mesh detection, and remeshing techniques [1]; Figure 2 portrays our finite element model along with the modeling outcomes. However, this quantification of uncertainty requires a clever Monte-Carlo-like approach that is computationally expensive. In other work, we have analyzed the mathematical model in terms of numerical stability [4, 6] and even considered microscale models [7, 8].
Can Machine Learning Make Mathematics Applicable in Clinics?
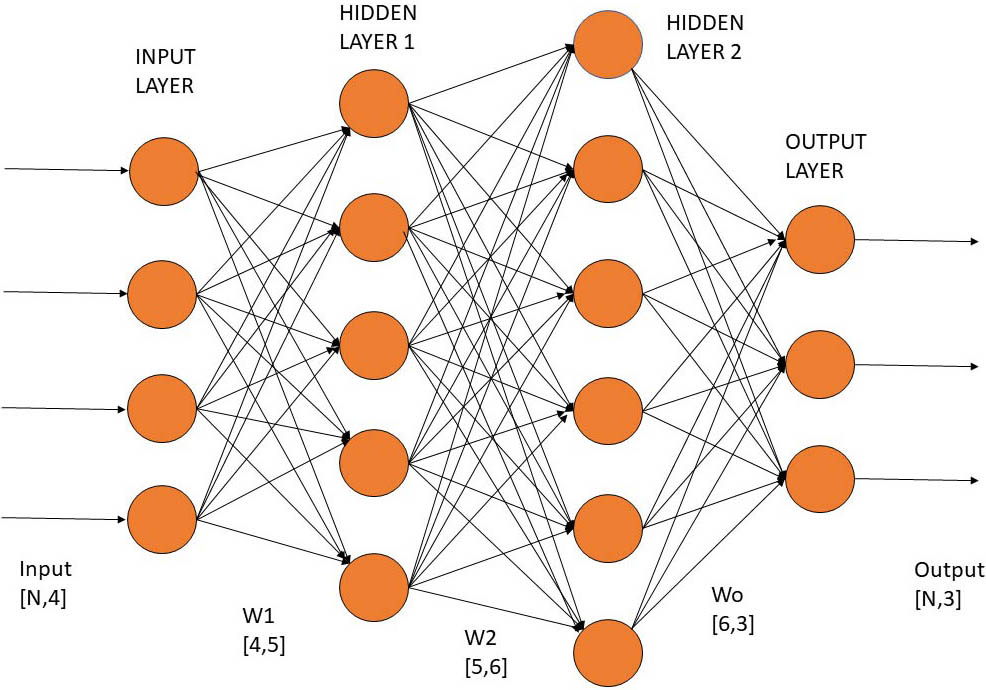
Complicated wound geometries require a multidimensional version of our model. And since each simulation in a multidimensional model is fairly computationally expensive, the finite-element-based estimation of the probability distributions for various post-burn scenarios under different therapies becomes unfeasible. We have therefore applied machine learning (ML) by training a neural network (NN) for wound geometries that previously could not be simplified. Figure 3 depicts a feed-forward NN that can reproduce the results from the finite-element-based model with very high accuracy. The \(R^2\)-factor for \(n\) data points yields a measure for the quality of reproductions of the finite element simulations via the ML framework. This \(R^2\)-factor is defined by \[R^2 = 1 - \frac{\displaystyle{\sum_{j=1}^n (y_j - \hat{y}_j )^2}}{\displaystyle{\sum_{j=1}^n (y_j - \overline{y})^2}},\tag3\]
where \(y_j\), \(\hat{y}_j\), and \(\overline{y}\) respectively represent the finite element data, NN-computed data, and arithmetic mean of the finite element data. We trained the NN to obtain \(R^2 > 0.9975\), which indicates very high fidelity [2, 5]. The ML-based model reproduces the degree of contraction, overall strain energy, and wound edge — allowing us to successfully follow the wound geometry over time. Since the computational speedup is roughly 1.8 million, the ML-based model quickly estimates the probability density of various scenarios in terms of the extent of contraction and total degree of patient agony. We therefore intend to further investigate the use of ML in order to provide clinicians with access to mathematical modeling simulations and results that can ultimately help to optimize treatments and therapies.
Fred Vermolen delivered a minisymposium presentation on this research at the 2023 SIAM Conference on Computational Science and Engineering, which took place earlier this year in Amsterdam, the Netherlands.
Acknowledgments: The authors acknowledge financial support from the Proefdiervrij foundation and the Dutch Burns Foundation (Nederlandse Brandwonden Stichting) in the framework of this project.
References
[1] Egberts, G., Desmoulière, A., Vermolen, F., & van Zuijlen, P. (2023). Sensitivity of a two-dimensional biomorphoelastic model for post-burn contraction. Biomech. Model. Mechanobiol., 22(1), 105-121.
[2] Egberts, G., Schaaphok, M., Vermolen, F., & van Zuijlen, P. (2022). A Bayesian finite-element trained machine learning approach for predicting post-burn contraction. Neural Comput. Appl., 34, 8635-8642.
[3] Egberts, G., Vermolen, F., & van Zuijlen, P. (2021). Sensitivity and feasibility of a one-dimensional morphoelastic model for post-burn contraction. Biomech. Model. Mechanobiol., 20(6), 2147-2167.
[4] Egberts, G., Vermolen, F., & van Zuijlen, P. (2021). Stability of a one-dimensional morphoelastic model for post-burn contraction. J. Math. Biol., 83(3), 24.
[5] Egberts, G., Vermolen, F., & van Zuijlen, P. (2023). High-speed predictions of post-burn contraction using a neural network trained on 2D-finite element simulations. Front. Appl. Math. Stat.: Insights Math. Biol., 9, 1098242.
[6] Egberts, G., Vermolen, F., & van Zuijlen, P. (2023). Stability of a two-dimensional biomorphoelastic model for post-burn contraction. J. Math. Biol., 86(4), 59.
[7] Peng, Q., Gorter, W., & Vermolen, F. (2022). Comparison between a phenomenological approach and a morphoelastic approach regarding the displacement of extracellular matrix. Biomech. Model. Mechanobiol., 21(3), 919-935.
[8] Peng, Q., & Vermolen, F. (2020). Agent-based modelling and parameter sensitivity analysis with a finite-element method for skin contraction. Biomech. Model. Mechanobiol., 19, 2525-2551.
[9] Stekelenburg, C.M., Simons, J.M., Tuinebreijer, W.E., & van Zuijlen, P.P.M. (2016). Analyzing contraction of full thickness skin grafts in time: Choosing the donor site does matter. Burns, 42(7), 1471-1476.
About the Authors
Fred Vermolen
Professor, University of Hasselt
Fred Vermolen is a full professor of computational mathematics at the University of Hasselt in Belgium. His research is in the field of free boundary problems, partial differential equations, numerical approaches, and uncertainty quantification, with applications in medicine and porous media. Vermolen was formerly an assistant and associate professor at the Delft University of Technology in the Netherlands.

Ginger Egberts
Postdoctoral researcher, Dutch Burns Foundation
Ginger Egberts is a postdoctoral researcher at the Dutch Burns Foundation in the Netherlands and the University of Hasselt in Belgium. Her research is in mathematical models for burn injuries and incorporates mathematical and numerical stability, feasibility, numerical implementation, and machine learning. Egberts obtained her Ph.D. from the Delft University of Technology in the Netherlands and the University of Hasselt.

Ibrahim Korkmaz
Postdoctoral researcher, Dutch Burns Center
Ibrahim Korkmaz is a postdoctoral researcher at the Dutch Burns Center and the Free University of Amsterdam Medical Center and Red Cross Hospital in the Netherlands. His research focuses on skin regeneration, immunology, and tissue function, and his approaches are both experimental and computational. Ibrahim has a background in biomedical and forensic sciences and holds a Ph.D. from the Free University of Amsterdam.

Paul van Zuijlen
Professor, Free University of Amsterdam
Paul van Zuijlen is an endowed professor at the Free University of Amsterdam and a plastic surgeon at the Dutch Burns Center and Red Cross Hospital in the Netherlands. His research focuses on burns, wounds, wound healing, reconstructive surgery, cartilage, plastic surgery, facial plastic surgery, head and neck surgery, surgical flaps, reconstruction, wound closure techniques, tissue expansion, wound dressings, burn units, pressure ulcers, electric burns, and chemical burns.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



