Optimizing Tissue Vascularization in Bioprinted Skin Grafts
As the largest organ in the human body, the skin protects internal organs from dangerous chemicals, extreme temperatures, and outside pathogens. Tissue engineering of skin grafts can help to heal and replace damaged skin, but several challenges complicate the process — especially in the context of full-thickness grafts for patients with major burns or non-healing ulcers [6]. The successful restoration of healthy tissue requires the careful selection of parameters for grafts and their internal channels, which allow blood to rapidly infiltrate the graft material and provide faster transport of necessary nutrients to cells. While controlling the properties of these channels and the associated bulk materials will certainly benefit the body’s response, researchers have not yet performed the required optimization or compared different engineering approaches in the field [9]. For example, since the channel diameter can change over time [10], altering the optimum initial channel size would improve the viability of graft cells. Important parameters include material composition, cross-linking structure or mesh size, water content, salinity, and thickness — all of which can considerably change the influence of swelling, the material’s degradation time [7], and the transport of blood and dissolved substances throughout the grafts [4, 5].
Experimental Methodology and Preliminary Results
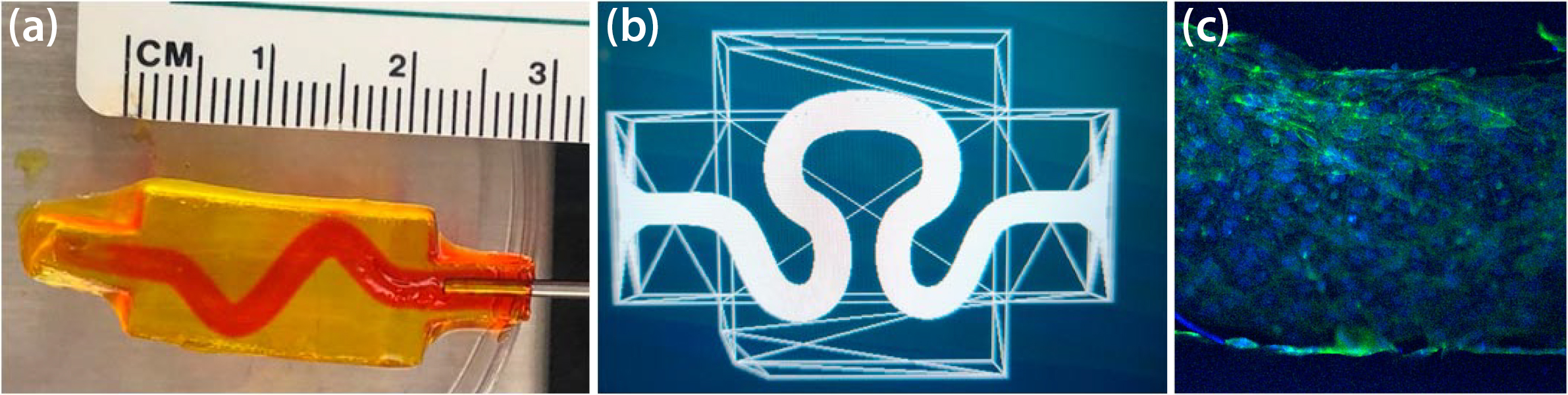
We prepared multiple different types of hydrogels—including hydrogels from gelatin methacrylate and polyethylene glycol diacrylate—to develop our experimental system and investigate parameters like template channel size, 3D printing techniques, and channel tortuosity (see Figures 1a and 1b). While these materials are common in the field and proposals for ideal parameters already exist, researchers rarely perform empirical predictions based upon experimental results; furthermore, these predictions are seldom valid if the hydrogel system changes. Even more important is the need to better understand time-dependent changes, such as channel diameter. We can both develop template channels in 3D-printed and cast hydrogels and grow a confluent layer of endothelial cells to coat the channel (see Figure 1c), which is important for the development of new blood vessels. Here, we use a Keyence microscope to rapidly image cells in different \(x\)-\(y\)-\(z\) positions and correlate with a computational model.
The Mathematical Model
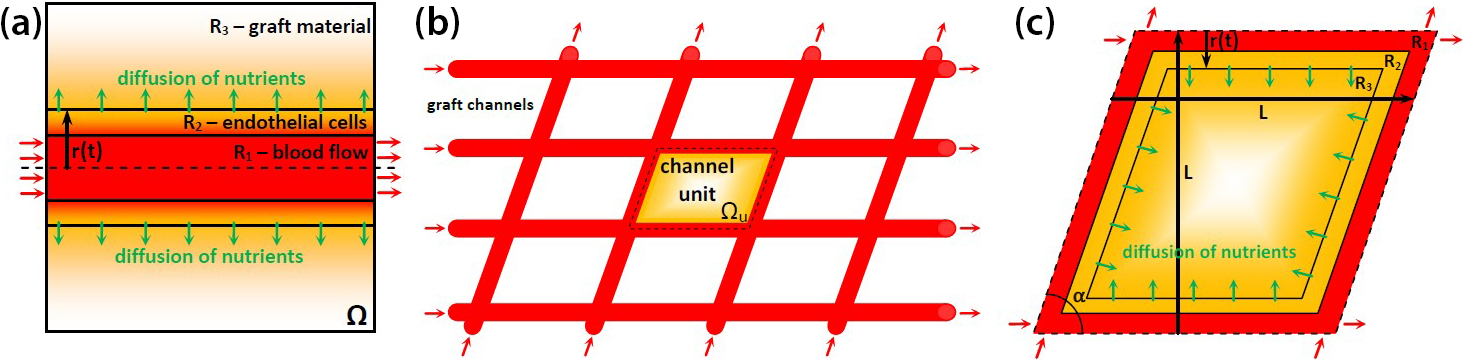
One of the main challenges when modeling the biophysics of vascularization via channels in the graft material is finding a suitable combination of physical laws to accurately approximate the underlying mechanisms of the modeled phenomena. To start, we identify a set of mathematical equations that can describe a model of the mass transport that is initiated by the blood flow in channels within the graft material. Our simple single-channel model in Figure 2a depicts three regions (\(R_1\), \(R_2\), and \(R_3\)) that respectively describe the channel with active blood flow, the endothelial cell layer, and the bulk graft material. To mimic the real behavior of biophysical mechanisms for applications in medical practice, future models will include additional channels and account for their interference in terms of nutrition transport outcomes. Figures 2b and 2c depict the established network of blood channels that is described by representative channel unit \(\Omega_u\). We aim to define the effective unit length \(L\), channel initial diameter \(d_0\), and angle of channel intersection \(\alpha\) as the design (optimization) parameters.
Modeling Flow Through a Porous Media
To model flows in the media that are characterized by porous structures—or porous-like formations in hydrogel-based materials—we must modify the classical formulation of the Navier-Stokes equation (subject to incompressibility and properly defined boundary and initial conditions):
\[\rho \left[ \frac{\partial{u}}{\partial{t}} + u \cdot \boldsymbol{\nabla} u \right] + \boldsymbol{\nabla} p - \boldsymbol{\nabla} \cdot \left[ \mu \boldsymbol{\nabla} u \right] + \chi_p \left[ \dfrac{\mu}{k} + \dfrac{\rho C_{ir}}{\sqrt{k}} |u| \right] u = 0.\]
The last term (a Forchheimer modification) adds resistance that is induced by the porous-like regions \(R_2\) and \(R_3\). Here, \(t\) is time, \(u(x,t)\) designates the velocity distribution, and \(p(x,t)\) represents the pressure field. Additional parameters describe the following fluid and material properties: density \(\rho\), dynamic viscosity \(\mu\), inertial resistance coefficient \(C_{ir}\), and “permeability” coefficient \(k\), which distinguishes different regions within domain \(\Omega\) and accommodates changes in flow permittivity over time. Finally, a characteristic function
\[\chi_p(x,t) = \left\{
\begin{aligned}
0, &\quad x \in \Omega_f\\
1, &\quad x \in \Omega_p
\end{aligned} \right.\]
switches between pore-free \(\Omega_f = R_1\) and porous \(\Omega_p = R_2 \cup R_3\) regions.
Modeling Nutrient Transport
The cells outside of the channel require nutrients from the blood or culture media flow. We assume the presence of \(m\) different nutrients (oxygen, glucose, etc.) and denote their concentrations by scalar functions \(C_i(x,t)\), \(i = 1, 2, \ldots, m\) as solutions of a system of diffusion partial differential equations (PDEs), which are again subject to suitable boundary and initial conditions:
\[\frac{\partial{C_i}}{\partial t} + u \cdot \boldsymbol{\nabla} C_i - \boldsymbol{\nabla} \cdot [ \gamma_i \boldsymbol{\nabla} C_i] + R_{c,i} = 0,\]
where \(\gamma_i\) is the diffusion coefficient of the \(i\)th nutrient. The consumption term
\[R_{c,i} = \beta_i N C_i\]
accounts for the decrease in concentration due to absorption. Here, \(\beta_i\) represents the consumption coefficients and \(N(x, t)\) is the cell density function. We assume that “alive” cells (re)produce when \(N < N_{\max}\) and “die” when \(C_i < C_d\). This reproduction is governed by the population ordinary differential equation:
\[\frac{\partial N}{\partial t} = \chi_s \lambda_p N ( N_{\max} - N) - (1-\chi_s) \lambda_d N, \qquad
\chi_s(C_i) = \left\{
\begin{aligned}
1, &\quad C_i \geq C_d,\\
0, &\quad C_i < C_d,
\end{aligned} \right.\]
where \(\lambda_p\), \(\lambda_d\), \(C_d\), and \(N_{\max}\) are parameters to calibrate.
Modeling Graft Material Properties
Our simplified model assumes that only two aspects trigger updates for medium properties: (i) swelling that affects channel radius
\[r(t; r_{\min}, S) = r_{\min} + (r_0 - r_{\min}) e^{-St}, \qquad r(t_0) = r_0,\]
and (ii) degradation (not yet implemented computationally)
\[k = k(t; D), \qquad C_{ir} = C_{ir}(t; D), \qquad \rho = \rho(t; D).\]
Here, \(r_{\min}\), \(S\), and \(D\) are again parameters to calibrate.
Initial Computational Results
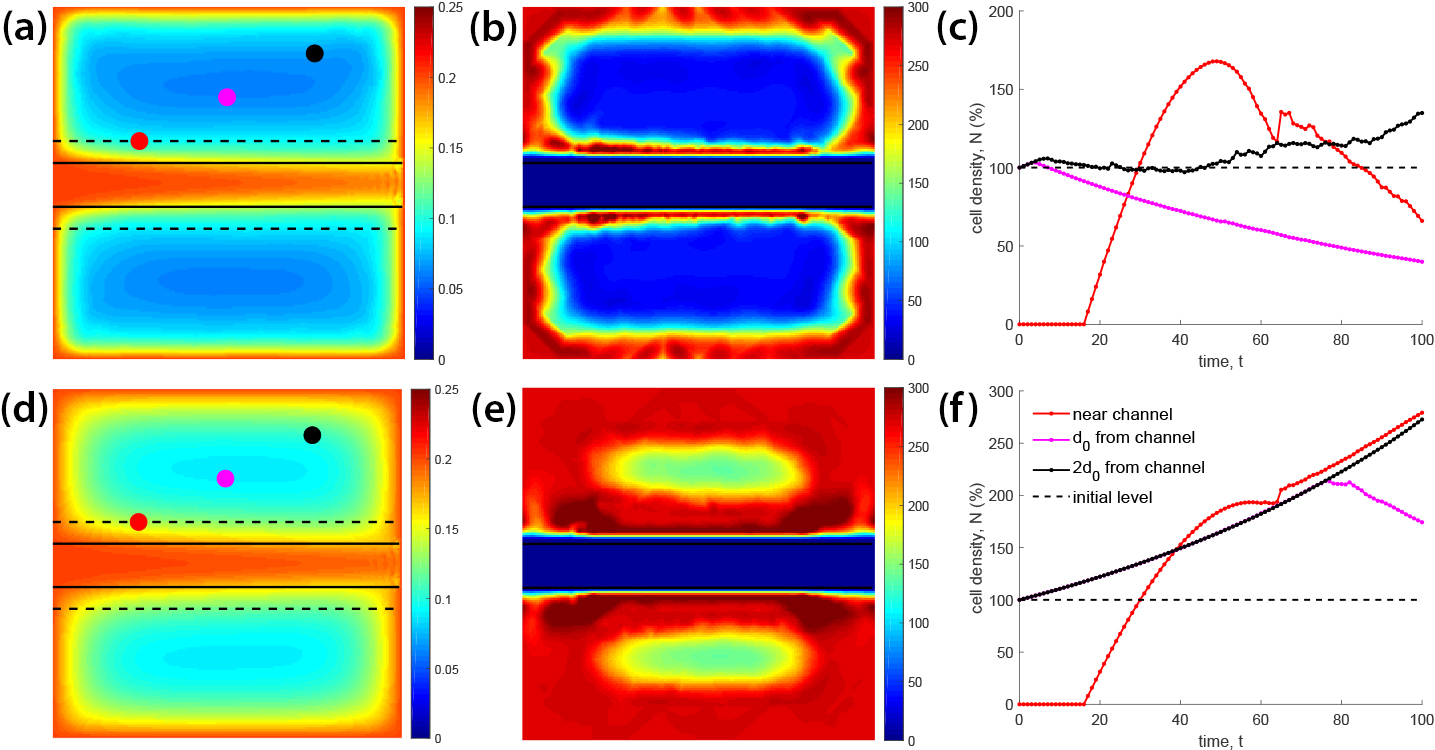
Figure 3 provides the first computational results for a two-dimensional toy problem with the model in Figure 2a. Figures 3a and 3d depict the concentration \(C = C_1(t_f)\) of one nutrient and Figures 3b and 3e depict the cell density \(N(t_f)\) at time \(t_f\) when the fields have reached equilibrium. We explore two situations that were characterized by high \((\beta = 0.25) \) and low \((\beta = 0.05) \) consumption rates, both with initial conditions \(C(t_0) = 0.2\) and \(N(t_0) = 1.0\). Despite its simplicity, this model offers valuable output in terms of future directions for the modeling and optimization (calibration) stages. For instance, Figures 3c and 3f illustrate the dynamics of cell density changes over time for both scenarios at different locations (depicted as dots in Figures 3a and 3d). Diversity is present in the profiles of these dynamics because the nutrient concentration is not uniformly distributed in the bulk material. This heterogeneity leads to unpredictable results and raises concerns about cell growth and viability in an engineered graft depending on consumption rate, blood velocity, material properties, channel geometry, and other parameters. We can control all of these parameters to optimize the effect on cell viability.
Computational Modeling and Optimization
Motivated by promising technology and preliminary modeling results, our future research will seek to utilize computational and optimization techniques to identify the ideal parameters of the 3D-bioprinted grafting material, such as cross-linking density and hydrogel material-water composition. We wish to create an efficient computational framework that supports mathematical and physical concepts by producing exhaustive computations for comprehensive, accurate models that represent the grafts’ primary biophysical phenomena. Modern optimization algorithms will enhance this framework and enable the search for optimal channel designs. We also intend to pursue a reliable methodology that promotes tissue vascularization by advising optimal channel geometry and material composition and structure to ensure nutrient transport throughout the graft. Ultimately, we hope that our advanced models will determine nutrient transport and cell growth in engineered grafts to facilitate healing for patients with skin injuries and nurture more viable cells within artificial grafts.
Vladislav Bukshtynov’s research group within the Department of Mathematics and Systems Engineering at the Florida Institute of Technology is exploring a complete suite of computational techniques to simulate physical and biological phenomena in the graft material with a prescribed channel structure, calibrate all parameters that govern these phenomena, and institute optimal channel design. These efforts combine various computational methods in areas like high-performance computing, highly nonlinear inverse problems, regularization, and multilevel parameterization. The optimization of both model calibration and design will adopt a methodology that reconstructs constitutive relations via system reduction techniques for systems of PDEs and incorporates a pioneering, four-dimensional variational method [1, 2]. We express the key elements of this approach—namely the gradients of the objective in the PDE-constrained optimization problem—in terms of integrals that are defined over the level sets of the state variable field. Although we have not yet applied this method in a bioengineering context, it has already found success in other classes of problems [1-3, 8].

Vladislav Bukshtynov delivered a contributed talk on this research at the 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), which took place in Tokyo, Japan, last year. He received funding to attend ICIAM 2023 through a SIAM Travel Award that was supported by U.S. National Science Foundation grant DMS-2233032. To learn more about SIAM Travel Awards and submit an application, visit the online page.
Acknowledgments: The authors would like to acknowledge the College of Engineering and Science (CoES) at the Florida Institute of Technology, particularly the CoES 2021 Institutional Research Incentive grant.
References
[1] Bukshtynov, V., & Protas, B. (2013). Optimal reconstruction of material properties in complex multiphysics phenomena. J. Comput. Phys., 242, 889-914.
[2] Bukshtynov, V., Volkov, O., & Protas, B. (2011). On optimal reconstruction of constitutive relations. Phys. D: Nonlinear Phenom., 240(16), 1228-1244.
[3] Danaila, I., & Protas, B. (2015). Optimal reconstruction of inviscid vortices. Proc. R. Soc. A, 471(2180), 20150323.
[4] Li, J., & Mooney, D.J. (2016). Designing hydrogels for controlled drug delivery. Nat. Rev. Mater., 1, 16071.
[5] Liao, H., Munoz-Pinto, D., Qu, X., Hou, Y., Grunlan, M.A., & Hahn, M.S. (2008). Influence of hydrogel mechanical properties and mesh size on vocal fold fibroblast extracellular matrix production and phenotype. Acta Biomater., 4(5), 1161-1171.
[6] MacNeil, S. (2007). Progress and opportunities for tissue-engineered skin. Nature, 445(7130), 874-880.
[7] Schwab, A., Levato, R., D’Este, M., Piluso, S., Eglin, D., & Malda, J. (2020). Printability and shape fidelity of bioinks in 3D bioprinting. Chem. Rev., 120(19), 11028-11055.
[8] Sethurajan, A.K., Krachkovskiy, S.A., Halalay, I.C., Goward, G.R., & Protas, B. (2015). Accurate characterization of ion transport properties in binary symmetric electrolytes using in situ NMR imaging and inverse modeling. J. Phys. Chem. B, 119(37), 12238-12248.
[9] Wen, N., Qian, E., & Kang, Y. (2021). Effects of macro-/micro-channels on vascularization and immune response of tissue engineering scaffolds. Cells, 10(6), 1514.
[10] Zhang, Y., Yu, Y., Akkouch, A., Dababneh, A., Dolati, F., & Ozbolat, I.T. (2015). In vitro study of directly bioprinted perfusable vasculature conduits. Biomater. Sci., 3(1), 134-143.
About the Authors
Beste Caner
M.S. Student, Florida Institute of Technology
Beste Caner is an M.S. student and the lab manager in the Department of Biomedical Engineering and Science at the Florida Institute of Technology.
Briana L. Edwards
Former Ph.D. student, Florida Institute of Technology.
Briana L. Edwards is a former Ph.D. student in the Department of Mathematical Sciences at the Florida Institute of Technology.
Nick Huynh
ReactDx
Nick Huynh is a former Ph.D. student in the Department of Biomedical and Chemical Engineering and Sciences at the Florida Institute of Technology. He currently works at ReactDx on the development of cardiac monitoring devices.
Chris Bashur
Associate Professor, Florida Institute of Technology
Chris Bashur is an associate professor in the Department of Chemistry and Chemical Engineering at the Florida Institute of Technology. His research focuses on the promotion of tissue vascularization, the development of new biomaterials, and the impact of these materials and the cellular microenvironment on functional engineered tissue.

Vladislav Bukshtynov
Assistant Professor, Florida Institute of Technology
Vladislav Bukshtynov is an assistant professor in the Department of Mathematics and Systems Engineering at the Florida Institute of Technology. He holds a Ph.D. in computational engineering and science from McMaster University and received the Cecil Graham Doctoral Dissertation Award in 2013 from the Canadian Applied and Industrial Mathematics Society. In 2023, Bukshtynov published a book titled Computational Optimization: Success in Practice. He also co-authored An Introduction to Partial Differential Equations with MATLAB with Matthew Coleman, which will appear in the summer of 2024.

Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



