Running in the Rain
What is the optimal speed of getting from \(A\) to \(B\) in the rain? By “optimal,” I mean picking up as little water as possible. Let’s ignore other considerations—such as the duration of discomfort weighted against the pain of running too fast—and assume that everything happens in two dimensions, and that the rain falls vertically. Given these assumptions, our connection to reality is of course tenuous.
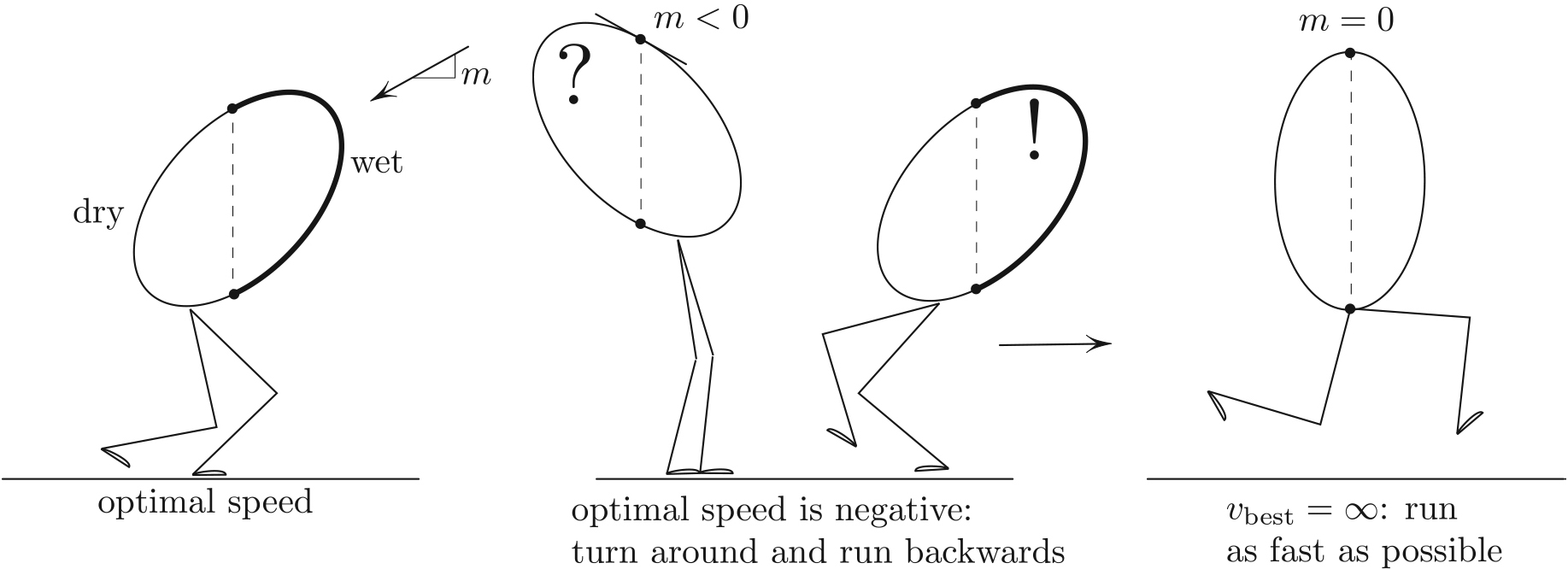
After recently getting caught in the rain, I realized that the above question has a clean geometrical answer: run with the speed at which the endpoints of the wet arc lie on the same vertical (see Figure 1). To restate this recipe, consider the longest vertical chord (dashed lines in Figure 1) and let \(m\) be the common slope of the tangents at the endpoints of this chord (these slopes are the same for the longest chord). The optimal speed is then such that the rain seems to be incoming at slope \(m\). Equivalently,
\[v_{\rm best}=\frac{v_{\rm rain}}{m}.\]
Explanation of the Recipe
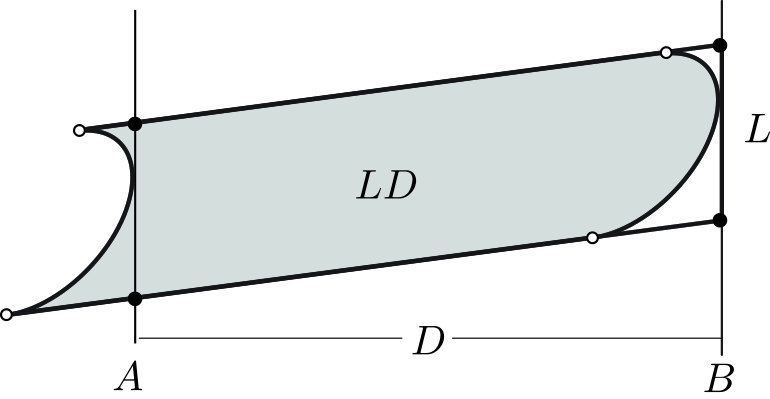
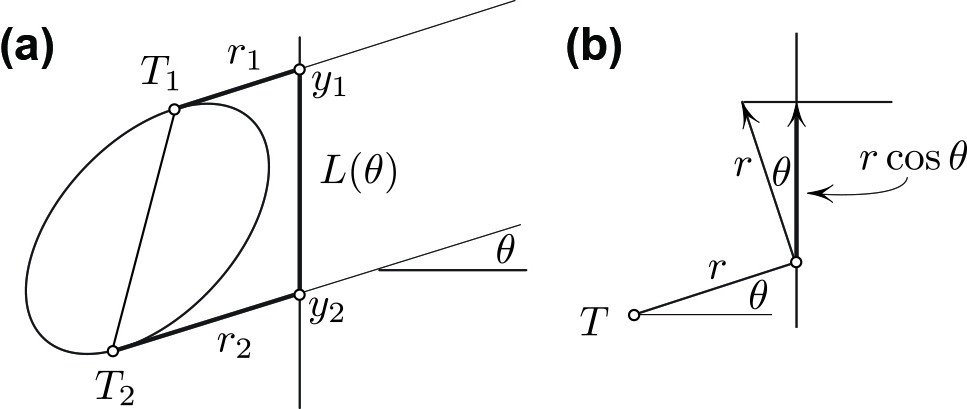
The amount of water that one picks up while running from \(A\) to \(B\) is proportional to the shaded area in Figure 2 swept by the “leading arc,” which in turn equals the area of the parallelogram \(LD\). Since \(D\) is fixed, our goal is to minimize \(L\) (see Figure 3). We will now show that \(L\) is minimized when the tangency points in Figure 3 lie on the same vertical. To that end, let us differentiate \(L\) with respect to \(\theta\) (see Figure 4):
\[L ^\prime ( \theta ) = y_1^\prime - y_2 ^\prime = r_1 \cos \theta - r_2 \cos \theta.\]
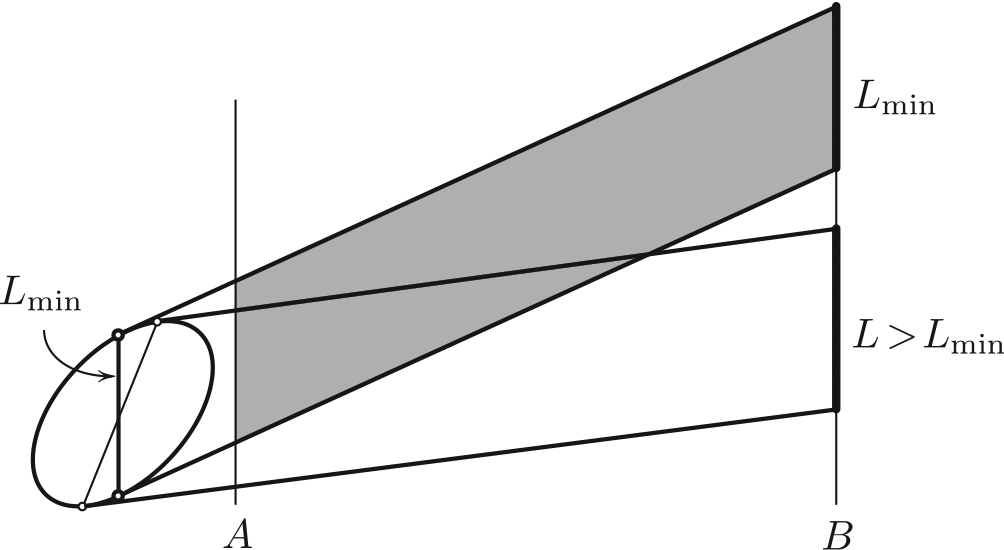
Figure 4b explains the last equality. The minimal \(L\) thus corresponds to \(r_1=r_2\), which is equivalent to the statement that \(T_1 T_2\) is vertical. This completes the justification of the recipe for the maximally dry run.
As a concluding remark, one of the standard calculus problems asks the aforementioned question in the case when the runner is a vertical segment. In this case, the contact points1 with the sloped lines are automatically on the same vertical. This holds for any slope, which means that the amount of water picked up is the same for any speed. Of course, this is clear directly from the fact that \(L\)—and thus the area \(LD\) of the parallelogram—does not depend on \(m\), and the reference to the recipe is not needed.
1 Counterparts of tangency points. I could have mentioned that the curve in Figure 1 can have corners, in which case we would speak of supporting lines instead of tangency lines.
The figures in this article were provided by the author.
About the Author
Mark Levi
Professor, Pennsylvania State University
Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



