Some Shallow Observations
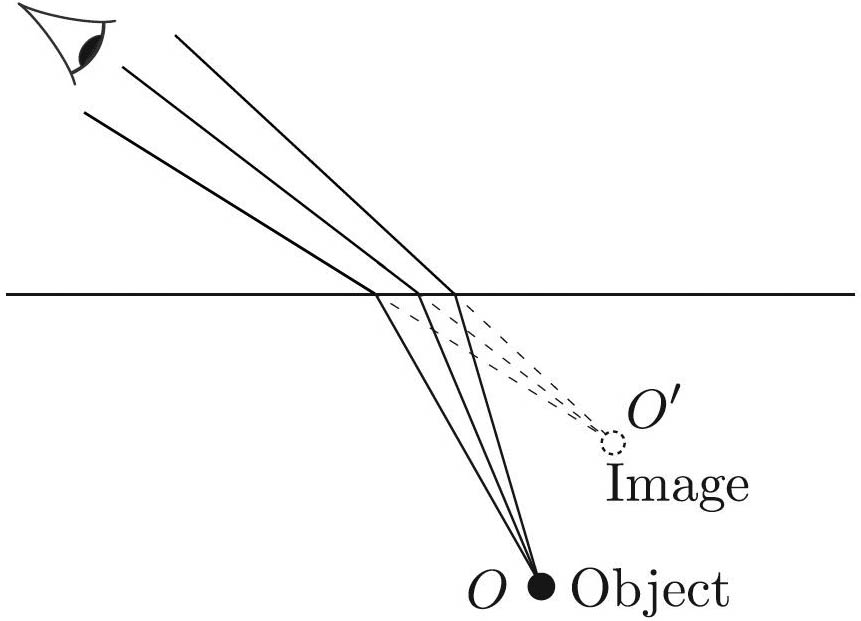
Water in a clear pool is deeper than it looks. What seems like five feet when looking straight down is actually seven feet — an unpleasant surprise for a non-swimmer. And this disparity between the true and apparent depths is quite striking for objects that are viewed at an angle. For example, when I direct my gaze 30 degrees below the horizontal, the true depth is more than five times greater than what I see!
Location of the Image
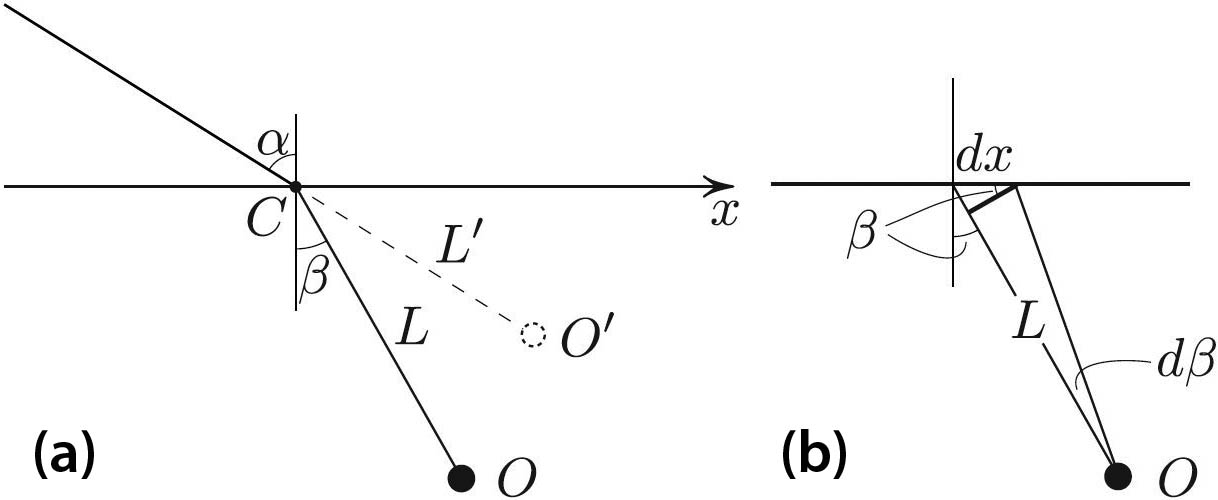
The image \(O ^{\prime}\) of the object \(O\) in Figure 1 is the apparent source of rays, i.e., the point from which the rays that reach the eye seem to emanate. To find the location of \(O {^\prime}\) given \(O\), let us advance the crossing point \(C\) in Figure 2 by a small distance \(dx,\) causing small changes in \(\alpha\) and \(\beta\). To the leading order of approximation, the length of the thick segment in Figure 2b can be expressed in two ways:
\[L\; d\beta = dx\; \cos \beta.\]
In a similar way, \(L ^{\prime} d\alpha = dx \; \cos \alpha\) and thus
\[\frac{L^{\prime}}{L} = \frac{\cos\alpha}{\cos\beta} \cdot \frac{d\beta}{d\alpha}.\tag1\]
To find \(d\beta/d\alpha\), we differentiate Snell’s law \(\sin \alpha/c_{\rm air} = \sin \beta/ c_{\rm water}\) to obtain
\[\frac{d\beta} {d\alpha} = c \frac{\cos\alpha}{\cos\beta},\]
where
\[c = c_{\rm water}/c_{\rm air} \approx 0.7,\]
the reciprocal of the refraction index. Substituting this into \((1)\) results in the nice expression
\[\frac{L ^\prime}{L} = c\; \frac{\cos ^2 \alpha}{\cos ^2 \beta}\tag2\]
for the ratio of the apparent length to the true length. This is the factor by which the underwater part of a tilted stick seems to shorten.1 Note that this shortening becomes drastic at oblique angles; for \(\alpha \uparrow \pi /2\), we have \(L ^{\prime}/L \rightarrow 0\).
Apparent Depth Versus True Depth
This ratio is given by an elegant expression that we obtain by dividing the apparent depth \(L ^{\prime} \cos \alpha\) by the true depth \(L \cos \beta\) and using \((2)\):
\[\frac{\hbox{apparent depth}}{\hbox{true depth}} = c\; \frac{\cos^3 \alpha }{\cos^3 \beta},\]
where \(c\) is as before. For example, the above ratio for \(\alpha = \pi/3\) is \(< 1/5\), a surprisingly small number; the water is more than five times deeper than it seems at that angle.
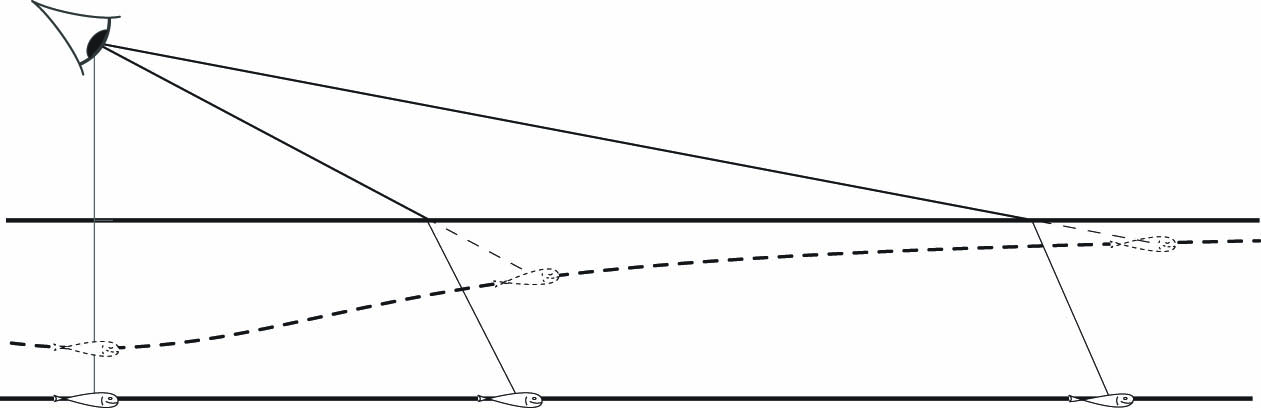
Distorted Images
Straight lines underwater do not look straight to the above observer (see Figure 3). A “dual” problem that may interest some students is to find the shape of the bottom whose image is straight (for the position of the eye fixed).
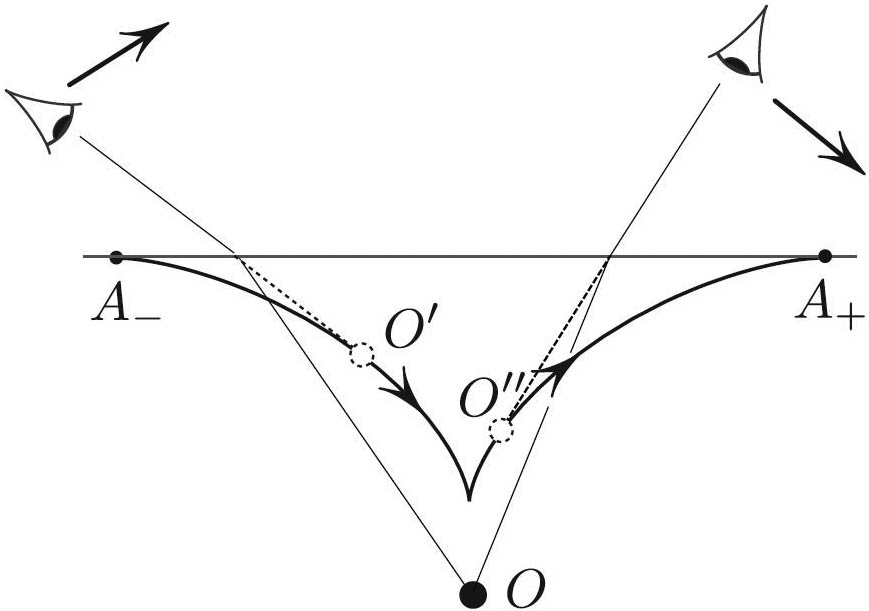
The Path of the Image
When the object \(O\) is fixed, all of its possible images for all viewers form a cusp (see Figure 4). As an observer swings around—as shown in the figure—the image travels along the caustic. The cusp’s shape varies homothetically with the depth of \(O\).
More Questions
With the eye’s position fixed, the map \(\varphi:= O \mapsto O^{\prime}\) of the lower half plane onto itself is well defined. It would be interesting to describe precisely how this map distorts small objects. That is, can we say something nice about the Jacobian of \(\varphi\)? What is its polar decomposition, for example? For my purposes here, however, that is going too deep.
1 Although it should be noted that the image of a straight stick isn’t quite straight, albeit not noticeably so.
The figures in this article were provided by the author.
About the Author
Mark Levi
Professor, Pennsylvania State University
Mark Levi (levi@math.psu.edu) is a professor of mathematics at the Pennsylvania State University.
Stay Up-to-Date with Email Alerts
Sign up for our monthly newsletter and emails about other topics of your choosing.



